La importancia de la teoría

Al igual que pasa con la música, son pocos los que en el mundo del sonido tienen conocimientos teóricos profundos de lo que se traen entre manos debido a que gran número de personas se aficionan sin pretensiones profesionales. En mi carrera al frente de una mesa de mezcla he podido trabajar con todo tipo de músicos. Algunos tenían más conocimientos "teóricos reglados" que otros y siempre he opinado que lo que prevalece ante todo es el talento. Ahora bien, es indudable que cuando un músico con talento adquiere cierto nivel de conocimiento teórico musical se convierte en una fuerza imparable de la naturaleza.

Por un lado, toman más soltura y rapidez (lo que conlleva a un aumento de la productividad musical) y por otra le permite usar un lenguaje con el que transmitir cosas complejas que de otra forma sería imposible hacer entender. A veces ni los propios músicos son conscientes de que van adquiriendo poco a poco conocimientos teóricos musicales, ya que se dan con ellos de frente a medida que van sumando experiencia. Por ejemplo, con un grupo con los que he trabajado en varios discos casi desde que empezaban a tocar he podido comprobar que con el paso de los años han ido desarrollando un lenguaje musical propio que tan solo ellos entienden y que describe muchas cosas que podríamos encontrar en libros sobre teoría musical. Los que se dedican a la música flamenca creo que son el máximo exponente de lo que os quiero decir. Hay que tener en cuenta que la música es un arte y como tal no es mejor artista el que más técnica y conocimiento tiene si no el que más "arte" demuestra.

En el mundo del sonido pasa un poco como con la música. A nadie le importa si el responsable de una grabación tiene más o menos conocimientos teóricos, sólo importa el resultado, pero, en mayor medida de lo que sucede en la música, los que habitamos los estudios de grabación nos damos de bruces con cuestiones teóricas casi desde el primer momento. Quien más y quien menos llega un a un punto en el que se ve en la necesidad de adquirir ciertos conocimientos para poder avanzar por muy básicos que estos sean. Por desgracia con el sonido y el audio nos topamos con un mundo físico/matemático donde conceptos como "miaja", que en música llegan a hacerse habituales, son demasiado ambiguos.

Yo siempre he pensado que el conocimiento teórico es un factor que potencia los conocimientos adquiridos con la experiencia. Algunas veces incluso llega a ser el primer paso con el que explorar nuevos caminos que nos llevarán a nuevas experiencias, llegando incluso a olvidar totalmente, por el hecho de tenerlos tan arraigados, que en su momento tuvimos que estudiar algunos conceptos básicos. Hace unos días mi sobrina de tres años me preguntó: "¿A qué no sabes que la M y la A hacen MA?". Ahora mismo tu estas leyendo esto que escribo, así que te harás una idea de lo que digo...

Mi idea es escribir una serie de artículos básicos sobre teoría de sonido y audio, los cuales en principio no va a ser necesario leer de forma secuencial. Si en alguna ocasión para entender uno de estos artículos fuese necesaria la lectura de otro ya lo indicaré mediante enlaces. Espero poder exponer de forma clara y concisa conceptos más o menos complejos tal que sean entendidos por gente sin amplios conocimientos de física ni de matemáticas. Mi intención es meramente divulgativa, y si os sirve como un primer paso para hacer una exploración más a fondo sobre alguno de los conceptos con los que trataremos o como texto corto para refrescar la memoria pues habré cumplido más funciones de las que originalmente tenía en mente.

Vamos a empezar esta serie de escritos con lo que podríamos considerar la "M+A=MA" en el mundo del sonido. Veamos algunos conceptos muy básicos tales como frecuencia, amplitud y periodo.

Onda sinusoidal, gráficas y funciones

Seguro que todos estáis acostumbrados a ver ondas sinusoidales en libros o foros de sonido. Si sois aficionados a los sintetizadores seguro, que vivís soñando con este tipo de señales.

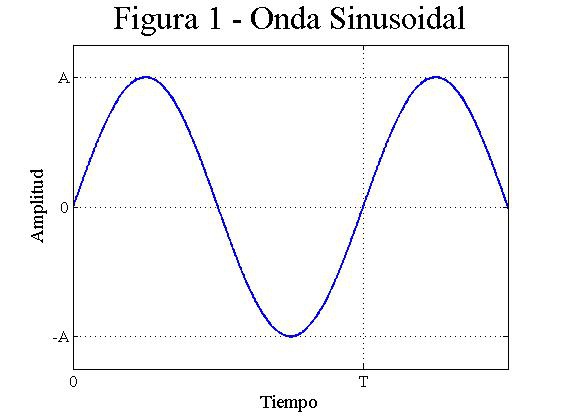
En la figura 1 podéis ver la representación gráfica de una onda sinusoidal. En realidad es tan sólo el dibujo en dos dimensiones de cómo varía la función seno en determinados valores de una variable (en nuestro caso el tiempo). Seguro que todo esto os suena a chino, pero es más fácil de lo que parece. Cuando veáis cualquier gráfica lo primero que debéis mirar es qué fenómeno representa. Si os fijáis bien en la gráfica de arriba en el eje Y tenemos la amplitud, mientras que en el eje X tenemos el tiempo. Por tanto es fácil saber que estamos ante la variación de amplitud que se produce en un determinado tiempo.

Normalmente os van a indicar qué medidas tienen; por ejemplo, en tiempo podemos encontrar segundos, y en amplitud casi cualquier cosa que os imaginéis (decibelios de algún tipo, presión sonora, voltage, intensidad eléctrica,...). Si os dais cuenta una gráfica así es la que podéis ver en cualquier DAW (Pro Tools, Nuendo, Cubase, Samplitude, ...). Estáis más que acostumbrados por tanto a ver representaciones de este tipo. En el eje Y, y puesto que cuando trabajamos con un DAW estamos en un ambiente digital , tendremos dBfs como medida de amplitud, mientras que en eje X tendremos el tiempo en la medida que tengáis seleccionada, como por ejemplo segundos o compases. De momento en vista de que es irrelevante para la explicación olvidemos eso. Simplemente diremos que hay amplitud y tiempo.

La función de arriba viene descrita por la siguiente ecuación:

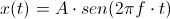
siendo A la amplitud máxima, f la frecuencia y t el tiempo.

Con tan solo esto ya podemos explicar muchos de los conceptos básicos con los que trabajamos en sonido.

Ciclo, período y frecuencia

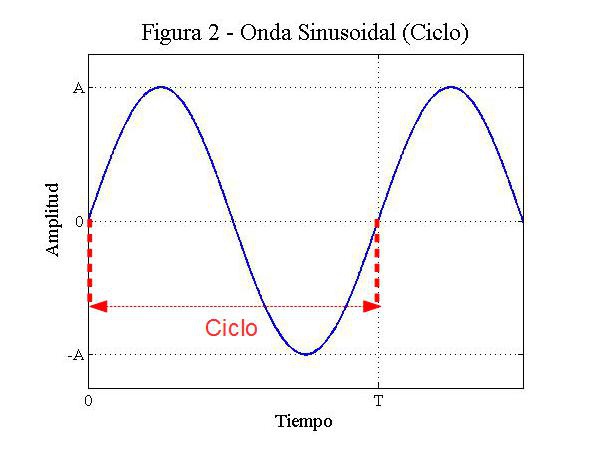
Lo primero que hay que tener claro es lo que significa ciclo. Cuando tratemos con señales que se repiten a lo largo del tiempo podemos definir un ciclo a todo lo que se comprenda desde el punto de inicio hasta que se vuelve al mismo punto en la misma condición. Es importante esto último, ya que no quiere decir que un ciclo se cumpla cuando tengamos el mismo valor de amplitud, si no cuando se empieza a repetir la forma dibujada. Por ejemplo en el la figura de la señal sinusoidal, si tomamos como el valor amplitud=0 como inicio vemos que la amplitud toma el valor 0 justo en la mitad. Por tanto un ciclo se cumple cuando se empieza otra vez el patrón de la señal. En la figura 3 podéis ver esto mejor.

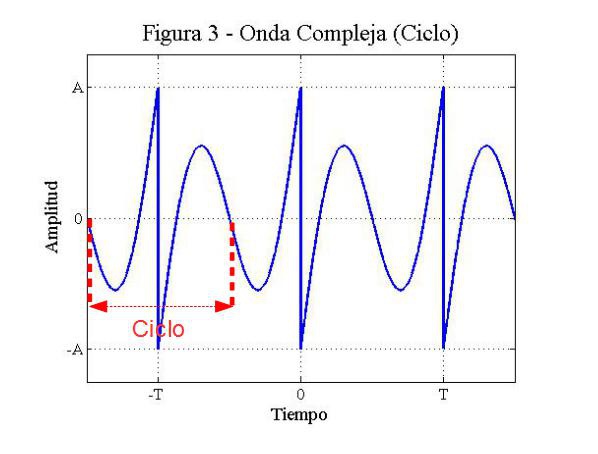
El periodo es el tiempo que se tarda en producirse un ciclo y la frecuencia es el número de ciclos que se se dan en un segundo. Como podéis imaginar el periodo y la frecuencia van a estar relacionadas. Cuanto menor sea el periodo más ciclos se van a dar en un segundo y por tanto mayor será la frecuencia.

La relación matemática entre frecuencia y periodo es la siguinte:

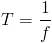
o dicho de otra manera:

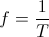
En la figura 4 podéis ver un ejemplo de todo esto. Ahí tenemos una onda cuyo ciclo tarda 0,01 segundo en producirse. Si tenemos en cuenta lo que hemos dicho antes su frecuencia será:

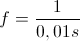
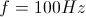
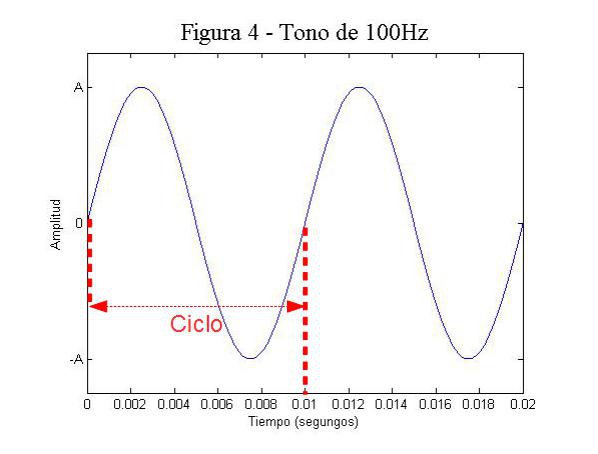
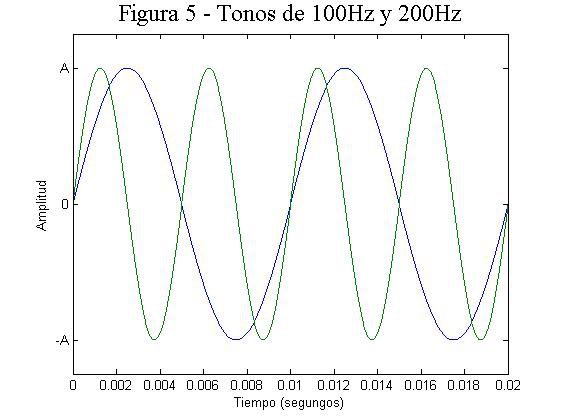
En la figura 5 podemos apreciar bien la relación que hay entre frecuencia y periodo. Vemos representados el tono de 100Hz que ya hemos visto (en azul) y un tono de 200Hz (en verde). Vemos que en el tiempo durante el cual el tono de 100Hz cumple un ciclo se cumplen dos ciclos del de 200Hz. Por tanto cuando comprobamos que cuando la frecuencia es mayor el tiempo necesario para que se cumpla un ciclo es menor. A mayor frecuencia tenemos periodos más cortos.

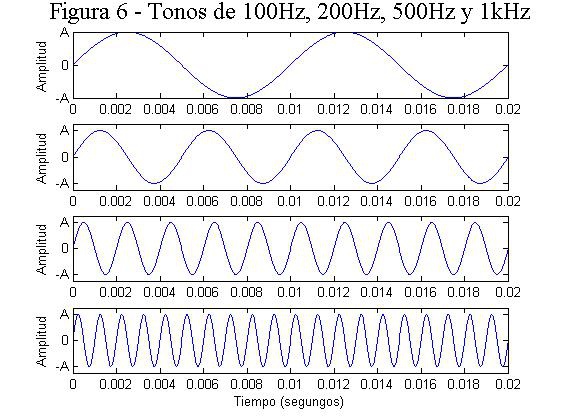
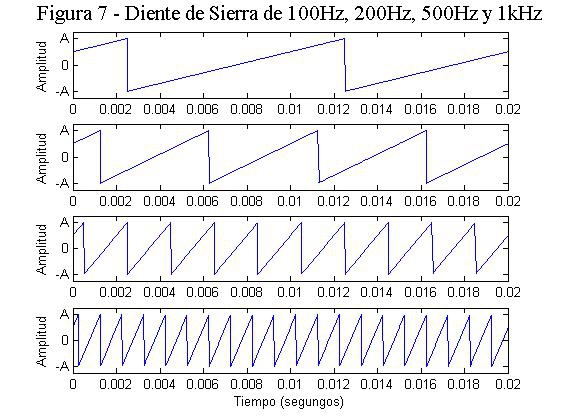
En las figuras 6 y 7 he representado dos tipos de señales (sinusoides y diente de sierra) y he ido aumentando la frecuencia para que podáis ver de forma fácil que el periodo disminuye.

Amplitud

Centrémonos ahora en la amplitud. Como ya hemos dicho la amplitud puede representar infinidad de cosas. Si estamos en acústica puede ser niveles SPL, niveles de potencia acústica,... si estamos trabajando con audio pueden ser dBfs si estamos en entorno digital, dBu si estamos en entornos analógicos,... Cuando llegue el momento en futuros artículo ya los veremos.

Si recordamos la ecuación que representa matemáticamente la onda sinusoidal que ya vimos antes la A es la que marcaba la amplitud máxima (o amplitud de pico) y la amplitud pico a pico es la amplitud comprendida entre el valor máximo y el valor mínimo. En la figura 8 podéis ver una representación gráfica de esto.

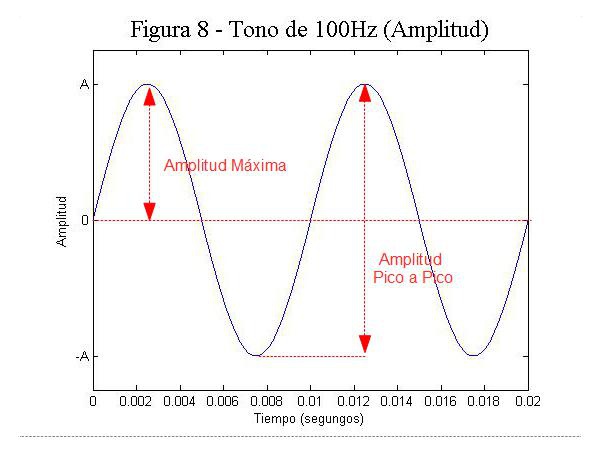
A nosotros la mayoría de veces nos va a importar la amplitud máxima o amplitud de pico y la amplitud eficaz o RMS. Mientras que la amplitud de pico nos va a permitir evitar saturaciones, el valor RMS es un buen indicador de la sonoridad (loudness). No voy a entrar en detalles de como se calcula la amplitud RMS ya que es bastante complejo y en realidad siempre vamos a tener programas informáticos que nos van a hacer el trabajo.

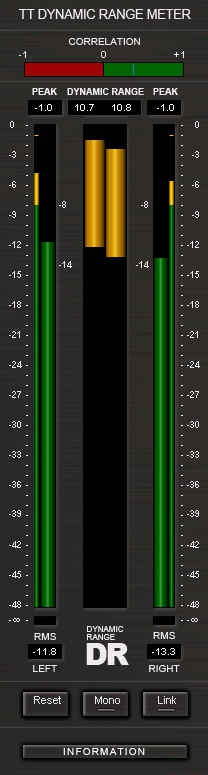
Plugin TT Dynamic Range Meter gratuito de Pleasurize Music Foundation.

Si recordamos la ecuación que definía a una señal sinusoidal llegados a este punto ya hemos explicado todo:

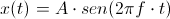
Sin embargo hay dos cuestiones importantes que añadir: la fase inicial y la amplitud inicial. Vamos a incluir estos dos factores en la ecuación:

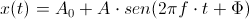
La amplitud inicial es lo que en el mundo del audio llamamos componente continua (DC offset en inglés), y el cual hay que evitar a toda costa. Normalmente se elimina por medio de un filtro paso alto.

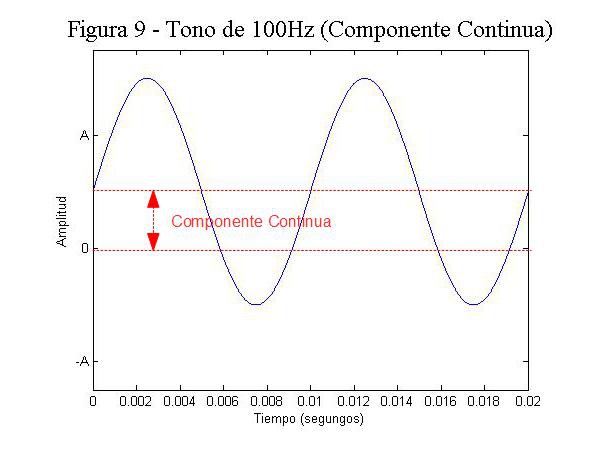
En la figura 9 podemos ver que al existir una componente continua en la señal se produce un desplazamiento (en este caso hacia arriba por ser una componente con valor positivo). Vamos a ver la problemática de esto con un ejemplo representado en la figura 10.

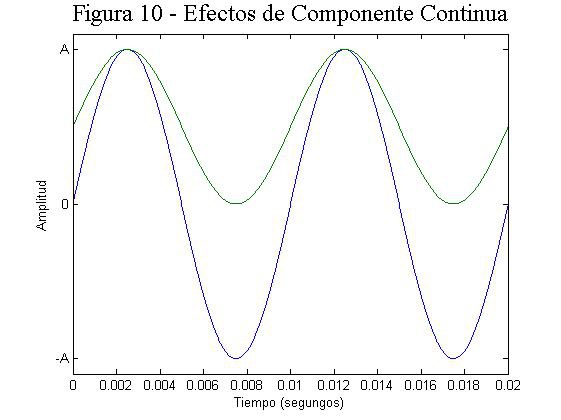
Imaginemos que tenemos una señal sinusoidal en un sistema donde todo lo que esté por encima de A va a saturar. Tomamos una señal sin componente continua (azul) y ajustamos su amplitud tal que su amplitud máxima llegue a A, que es donde nuestro sistema satura. Ahora tomamos una señal cuya componente continua tiene un valor de A/2 (verde) y hacemos lo mismo, ajustamos su amplitud hasta que lleguemos al valor máximo A. Vemos la señal azul tiene una amplitud pico a pico mucho mayor que la verde, aun cuando en ambas señales tengan su pico en la amplitud máxima A. Por tanto vemos que una señal que posee componente continua vera su valor RMS mermado, ya que aun cuando tengamos un valor alto de pico el valor pico a pico va a ser menor que en condiciones libres de componente continua.

Si la amplitud inicial hace referencia a un desplazamiento de la señal en cuanto a la amplitud, la fase inicial hace referencia a un desplazamiento de la señal en el tiempo. Este desfase viene expresada normalmente en grados, aunque en audio es muy normal hablar de desfases en segundos.

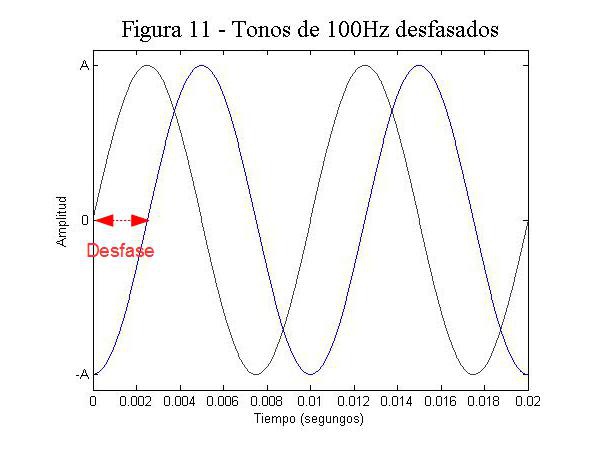
Como hemos dicho, los desfases vienen dados también en grados. Esto se debe a que en realidad la frecuencia puede representarse en frecuencia angular. No profundizaré en esto de momento, aunque seguro que lo haré en futuros artículos. Tampoco haré más análisis del desfase ya que aquí mismo en Hispasonic tenéis dos artículos muy completos sobre este fenómeno escritos por Pablo Fernández-Cid. Los podéis encontrar aquí:

Fase: la cara oculta del audio.

Fase: la cara oculta del audio (II).

Si habéis llegado hasta aquí ¡ENHORABUENA! Espero que asimiléis bien estos conceptos que, aunque al principio se hacen aburridos, son necesarios para en un futuro poder entender otros artículos más interesantes. Espero que os enganchéis y me acompañéis en ellos.

Autor: José A. Medina (2013)